Последние конференции
- Информационные системы и модели в научных исследованиях, промышленности, образовании и экологии
- Информационные системы и модели в научных исследованиях, промышленности и экологии
- Современные проблемы экологии
- Экологические проблемы окружающей среды, пути и методы их решения
- Экология, образование и здоровый образ жизни
О непараметрической идентификации стохастических систем
А.А. Корнеева, Н.А. Сергеева, Е.А. Чжан
Сибирский Федеральный Университет,
г. Красноярск
Введение. Безусловно, проблема моделирования, идентификации надолго останется одной из центральных проблем кибернетики. При формулировке задач идентификации и управления особую роль играет уровень априорной информации. Она зависит как от имеющихся средств контроля, так и от самой технологии измерения переменных. Более того, отличие в средствах контроля неизбежно будет приводить к различным постановкам задач идентификации и моделирования даже для процессов одного и того же типа.
На практике дискретность измерения «входных–выходных» переменных исследуемого процесса может не совпадать. В результате матрица наблюдений состоит из не полностью заполненных строк, как по входным, так и по выходным переменным. Отсюда возникает проблема восстановления пропусков в незаполненных строках матрицы наблюдений.
Постановка задачи. Приведем достаточно общую схему исследуемого процесса:
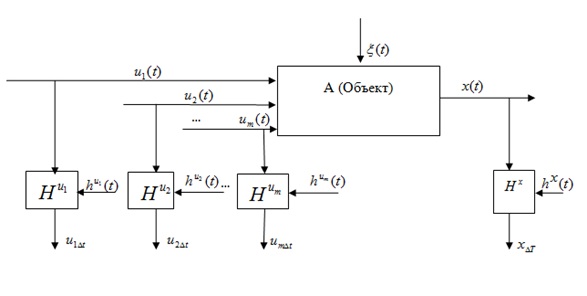
Рис.1. Общая схема исследуемого процесса
На рис.1 приняты обозначения: А – неизвестный оператор объекта, ![]() – векторная выходная переменная процесса,
– векторная выходная переменная процесса, ![]() – векторное управляющее воздействие,
– векторное управляющее воздействие, ![]() – векторное случайное воздействие, (
– векторное случайное воздействие, (![]() ) – непрерывное время,
) – непрерывное время, ![]() ,
, ![]() – каналы связи, соответствующие различным переменным, включающие в себя средства контроля. Контроль
– каналы связи, соответствующие различным переменным, включающие в себя средства контроля. Контроль ![]() осуществляется через интервал времени
осуществляется через интервал времени ![]() , контроль
, контроль ![]() через
через ![]() , причем
, причем![]() .
. ![]() ,
, ![]() – случайные помехи измерений соответствующих переменных процесса с нулевыми математическими ожиданиями и ограниченной дисперсией.
– случайные помехи измерений соответствующих переменных процесса с нулевыми математическими ожиданиями и ограниченной дисперсией.
Идентификация в «узком» и «широком» смыслах. При моделировании разнообразных дискретно-непрерывных процессов в настоящее время доминирует теория идентификации в «узком» смысле [1, 2]. Ее содержание состоит в том, что на первом этапе на основании имеющейся априорной информации определяется параметрический класс операторов ![]() , например,
, например,
![]() (1)
(1)
где ![]() – параметрическая структура модели, а
– параметрическая структура модели, а ![]() – вектор параметров. На втором этапе осуществляется оценка параметров
– вектор параметров. На втором этапе осуществляется оценка параметров ![]() на основе имеющейся выборки
на основе имеющейся выборки ![]() , s – объем выборки. Успех решения задачи идентификации в этом случае существенно зависит от того, насколько «удачно» определен оператор (1).
, s – объем выборки. Успех решения задачи идентификации в этом случае существенно зависит от того, насколько «удачно» определен оператор (1).
Идентификация в «широком» смысле предполагает отсутствие этапа выбора параметрического класса оператора. Часто оказывается значительно проще определить класс операторов на основе сведений качественного характера, например, линейности процесса или типа нелинейности, однозначности либо неоднозначности и др. В этом случае задача идентификации состоит в оценивании этого оператора на основе выборки ![]() в форме
в форме
![]() (2)
(2)
где ![]() – временные векторы.
– временные векторы.
Методика заполнения матрицы наблюдений. Пусть дана выборка, состоящая из ![]() независимых наблюдений случайных величин
независимых наблюдений случайных величин ![]() , при наличии случайных помех в каналах измерения. Представляет интерес задача, связанная с восстановлением недостающих измерений переменных в матрице наблюдений. Можно представить исходные измерения переменных в Табл.1.
, при наличии случайных помех в каналах измерения. Представляет интерес задача, связанная с восстановлением недостающих измерений переменных в матрице наблюдений. Можно представить исходные измерения переменных в Табл.1.
Таблица 1
|
u1 |
u2 |
… |
um |
x |
|
u11 |
u21 |
… |
um1 |
x1 |
|
u12 |
u22 |
… |
um2 |
|
|
u13 |
u23 |
… |
um3 |
|
|
u14 |
u24 |
… |
um4 |
x4 |
|
… |
… |
… |
… |
… |
|
u1s |
u2s |
… |
ums |
xs |
Для восстановления пропусков значений ![]() в Табл.1 использовалась обычная непараметрическая оценка [4] регрессии:
в Табл.1 использовалась обычная непараметрическая оценка [4] регрессии:
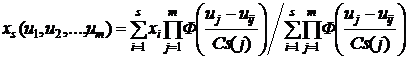 , (3)
, (3)
где ![]() – ядерная колоколообразная функция и коэффициент размытости ядра
– ядерная колоколообразная функция и коэффициент размытости ядра ![]() удовлетворяют некоторым условиям сходимости [3, 4].
удовлетворяют некоторым условиям сходимости [3, 4].
Этапы восстановления пропусков матрицы наблюдений. Алгоритм восстановления пропусков матрицы наблюдений можно разделить на три этапа [5]. На первом этапе алгоритма восстанавливается функция регрессии ![]() по наблюдениям, полностью представленным в исходной матрице измерений, то есть по полностью заполненным строкам в результате эксперимента (Табл.1). Оптимальное значение коэффициента
по наблюдениям, полностью представленным в исходной матрице измерений, то есть по полностью заполненным строкам в результате эксперимента (Табл.1). Оптимальное значение коэффициента ![]() подбирается в режиме скользящего экзамена при минимизации квадратичной ошибки аппроксимации. На втором этапе происходит заполнение пропусков
подбирается в режиме скользящего экзамена при минимизации квадратичной ошибки аппроксимации. На втором этапе происходит заполнение пропусков ![]() в матрице наблюдений (Табл.1) c использование оценки
в матрице наблюдений (Табл.1) c использование оценки ![]() и оптимального значения коэффициента размытости ядра
и оптимального значения коэффициента размытости ядра ![]() , полученных на предыдущем этапе. Там, где наблюдения
, полученных на предыдущем этапе. Там, где наблюдения ![]() пропущены, в оценку
пропущены, в оценку ![]() подставляем значения измеренных
подставляем значения измеренных ![]() и вычисляем соответствующую оценку
и вычисляем соответствующую оценку ![]() , которой восполняем недостающее наблюдение
, которой восполняем недостающее наблюдение ![]() (например, недостающая
(например, недостающая ![]() в представленной выше матрице наблюдений заполняется значением
в представленной выше матрице наблюдений заполняется значением ![]() ). После этого этапа матрица наблюдений принимает следующий вид:
). После этого этапа матрица наблюдений принимает следующий вид:
Таблица 2
|
u1 |
u2 |
… |
um |
x |
|
u11 |
u21 |
… |
um1 |
x1 |
|
u12 |
u22 |
… |
um2 |
xs2 |
|
u13 |
u23 |
… |
um3 |
xs3 |
|
u14 |
u24 |
… |
um4 |
x4 |
|
… |
… |
… |
… |
… |
|
u1s |
u2s |
… |
ums |
xs |
Заключительный этап восстановления зависимости ![]() от
от ![]() состоит в построении непараметрической оценки по всей имеющейся (заполненной) матрице наблюдений (Табл.2).
состоит в построении непараметрической оценки по всей имеющейся (заполненной) матрице наблюдений (Табл.2).
Вычислительный эксперимент. Для численного исследования был выбран объект, имеющий три входа ![]() и один выход
и один выход ![]() . Пусть нам известно лишь каждое третье от всех значений выхода,
. Пусть нам известно лишь каждое третье от всех значений выхода, ![]() , то есть матрица наблюдений может быть представлена в виде Табл.1. Зададим уравнения объекта, отличающиеся степенью нелинейности:
, то есть матрица наблюдений может быть представлена в виде Табл.1. Зададим уравнения объекта, отличающиеся степенью нелинейности:
![]() ;
; ![]() . (4)
. (4)
При моделировании в «узком» смысле эксперимент осуществлялся в два этапа. На первом мы «угадали» верную структуру объекта, на втором – заведомо допустили ошибку.
При совпадающих структурах, как при использовании исходной матрицы с пропусками, так и при использовании восстановленной матрицы, получили одинаково хороший результат для всех исследуемых структур.
На втором этапе данного эксперимента мы специально допустили ошибку в выборе структуры модели. Для исследования выбран объект ![]() из (4). Поочередно было исследовано три структуры модели:
из (4). Поочередно было исследовано три структуры модели:
![]() , (5)
, (5)
![]() , (6)
, (6)
![]() . (7)
. (7)
Во всех трех случаях отличие между объектом и моделью заключается лишь в коэффициенте при ![]() в аргументе синуса.
в аргументе синуса.
В результате моделирования были получены следующие результаты для уже заполненной матрицы. Для уравнения (5) ошибка моделирования ![]() в условиях без помех составила 46 %, при помехах 5 % и 10 % ошибка составила соответственно 49 % и 51 %. Для структуры (6) эти показатели равны 31 %, 34 %, 38 %. Для структуры (7), которая практически не отличается от структуры объекта моделирования
в условиях без помех составила 46 %, при помехах 5 % и 10 % ошибка составила соответственно 49 % и 51 %. Для структуры (6) эти показатели равны 31 %, 34 %, 38 %. Для структуры (7), которая практически не отличается от структуры объекта моделирования ![]() , получили значения 9 %, 13 %, 19 %.
, получили значения 9 %, 13 %, 19 %.
На рис.2 графически проиллюстрированы результаты численного эксперимента для уравнения модели (6) при помехе 5 %.
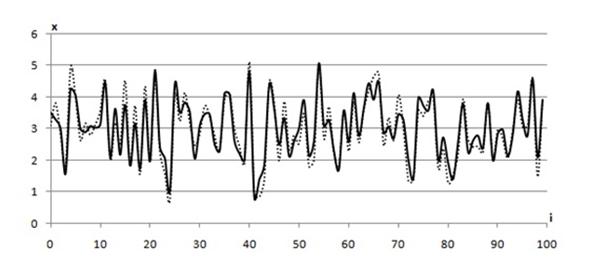
Рис.2. Выход объекта и модели
По графикам видно значительное отклонение движения модели (пунктир) от объекта (сплошная линия) при неточной параметризации модели.
Исследование при идентификации в «широком» смысле состоит из двух этапов. Сначала непараметрическая оценка регрессии строится по исходной матрице наблюдений с пропусками (Табл.1), затем – по заполненной (Табл.2). Для уравнения объекта ![]() из (4) при объеме выборки
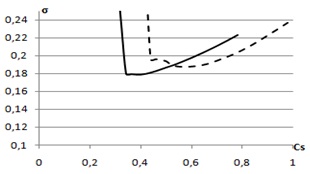
из (4) при объеме выборки ![]() = 1000 были получены следующие результаты. При использовании матрицы с пропусками ошибка моделирования составляет в среднем 15 %, в то время как оценивание по заполненной матрице дает ошибку в 12%. При уровне помех в 5 % данное соотношение составляет в среднем 17 % к 14 %, при помехе в 10 % - 23 % к 21 %. Рис. 3 графически иллюстрирует процедуру выбора оптимального коэффициента
= 1000 были получены следующие результаты. При использовании матрицы с пропусками ошибка моделирования составляет в среднем 15 %, в то время как оценивание по заполненной матрице дает ошибку в 12%. При уровне помех в 5 % данное соотношение составляет в среднем 17 % к 14 %, при помехе в 10 % - 23 % к 21 %. Рис. 3 графически иллюстрирует процедуру выбора оптимального коэффициента ![]() . Из него видно, что значение ошибки моделирования
. Из него видно, что значение ошибки моделирования ![]() при оптимальном
при оптимальном ![]() для оценки, полученной по заполненной матрице, меньше, чем ошибка по незаполненной (пунктирной линией обозначена модель, построенная по исходной матрице).
для оценки, полученной по заполненной матрице, меньше, чем ошибка по незаполненной (пунктирной линией обозначена модель, построенная по исходной матрице).
|
Рис.3. Выбор оптимального Cs
|
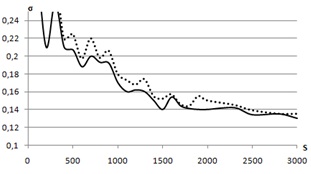
Рис.4. Зависимость ошибки от S |
На рис.4 показана зависимость ошибки моделирования ![]() от объема выборки
от объема выборки ![]() . Пунктирной линией показана модель, построенная по исходной матрице, сплошной – по заполненной. По данному рисунку можно сделать следующие вывод: ошибка по заполненной матрице на всем рассмотренном объеме оказывается меньше ошибки по исходной матрице.
. Пунктирной линией показана модель, построенная по исходной матрице, сплошной – по заполненной. По данному рисунку можно сделать следующие вывод: ошибка по заполненной матрице на всем рассмотренном объеме оказывается меньше ошибки по исходной матрице.
Заключение. Рассмотрена задача восстановления матрицы наблюдений с пропусками для решения задачи идентификации стохастических, статических объектов. Предложена методика восстановления пропусков матрицы наблюдений и приведены соответствующие алгоритмы. Показано, что задача идентификации по заполненной матрице решается более точно, чем по незаполненной, что иллюстрируют численные эксперименты.
Список литературы
1. Цыпкин, Я.З. Основы информационной теории идентификации – М.: Наука, 1984. – 320 с.
2. Эйкхофф, П. Основы идентификации систем управления – М.: Мир, 1975. – 683 с.
3. Медведев А.В. Непараметрические системы адаптации. – Новосибирск, Наука, 1983. – 174с.
4. Надарая Э.А. Непараметрические оценки плотности вероятности и кривой регрессии. – Тбилиси: изд. Тбил. ун-т, 1983. – 194 с.
А.А.Корнеева, Н.А.Сергеева. О непараметрическом восстановлении матрицы наблюдений с пропусками в задаче оценки функции регрессии/ Материалы XV-ой Международной конференции «Решетневские чтения»// Красноярск: изд-во СибГАУ, 2011. – с. 458-459.